CHARACTERISTICS OF SOLAR CELLS
Equivalent Circuit Of A Solar Cell
To understand the electronic
behavior of a solar cell, it is useful to create a model which is electrically
equivalent, and is based on discrete electrical components whose behavior is
well known.

Fig3.1.1 Equivalent Circuit Of Solar Cell
|
1 Characteristic equation
From the equivalent circuit it is
evident that the current produced by the solar cell is equal to that produced by the current source, minus that
which flows through the diode, minus that which flows through the shunt resistor
I = IL − ID − ISH
Where,
I =output current (amperes)
IL = output generated current (amperes)
ID = diode current
(amperes)
ISH = shunt current (ampers)
The current through these
elements is governed by the voltage across them:
Vj = V+IRS
Where,
Vj = voltage across both diode and resistor RHS (volts)
V = voltage across the output terminals (volts)
I =output current (amperes)
Rs = series resistance (Ω)
By the Shockley diode equation,
the current diverted through the diode is:
Where,
Io = reverse saturation current (amperes)
n = diode ideality factor (1 for an ideal diode)
q = elementary charge
k = Boltzmann's constant
T = absolute temperature
By Ohm's law, the current diverted through the shunt resistor is:
2 Open-circuit voltage and short-circuit current
When the cell is operated at open circuit, I = 0 and the voltage across the output terminals is defined as the open-circuit voltage. Assuming the shunt resistance is high enough to neglect the final term of the characteristic equation, the open-circuit voltage VOC is:
Similarly, when the cell is operated at short circuit, V = 0 and the current I through the terminals is defined as the short-circuit current. It can be shown that for a high-quality solar cell (low RS and I0, and high RSH) the short circuit current ISC is:
The values of I0, RS, and RSH are dependent upon the physical size of the solar cell. In Comparing otherwise identical cells, a cell with twice the surface area of another will, in Principle, have double the I0 because it has twice the junction area across which current can leak. It will also have half the RS and RSH because it has twice the cross-sectional area
Through which current can flow. For this reason, the characteristic equation is frequently written in terms of current density, or current produced per unit cell area:
where,
J = current density (amperes/cm2)
JL = photo generated current density (amperes/cm2)
Jo = reverse saturation current density (amperes/cm2)
rs = specific series resistance (Ω-cm2)
rSH = specific shunt resistsnce (Ω-cm2)
formulation has several advantages. One is that since cell characteristics are referenced to a common cross-sectional area they may be compared for cells of different physical dimensions. While this is of limited benefit in a manufacturing setting, where all cells tend to be the same size, it is useful in research and in comparing cells between manufacturers. Another advantage is that the density equation naturally scales the parameter values to similar orders of magnitude, which can make numerical extraction of them simpler and more accurate even with naive solution methods.
This formulation has several advantages. One is that since cell characteristics are referenced to a common cross-sectional area they may be compared for cells of different physical dimensions. While this is of limited benefit in a manufacturing setting, where all cells tend to be the same size, it is useful in research and in comparing cells between manufacturers. Another advantage is that the density equation naturally scales the parameter values to similar orders of magnitude, which can make numerical extraction of them simpler and more accurate even with naive solution methods.
A practical limitation of this formulation is that as cell sizes shrink, certain parasitic effects grow in importance and can affect the extracted parameter values so very small cells may exhibit higher values of J0 or lower values of rSH than larger cells that are otherwise identical. In such cases, comparisons between cells must be made cautiously and with these effects in mind
3I-V Curve of Solar Cell
PV cells can be modeled as a current source in parallel with a diode. When there is no light present to generate any current, the PV cell behaves like a diode. As the intensity of incident light increases, current is generated by the PV cell, as illustrated in Figure.
 |
2 V-I and P-V curve of solar cell
|
 |
| 3 I-V curve of an illuminated PV cell |
Thank you for visit our website. "armaelectrical.com"







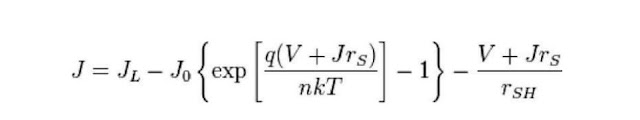







0 Comments